Bayesian updates to multi-age Antarctic sea-ice concentrations using GNSS-R data

Speaker: Steefan Contractor

Coauthors: Shane Keating (UNSW), Jessica Cartwright (Spire Global), Alex Fraser (UTAS)

Sea Ice

  • Floating ice that forms from the freezing of seawater
  • Melting and formation of sea ice affects the ocean salinity and heat content
  • The changes in ocean density and temperature affect the ocean circulation as evidenced by recent coverage on AMOC weakening
  • It affects the Earth’s energy balance by reflecting ten times more sunlight compared to water
  • It acts like a blanket affecting not just heat exchange between the ocean and atmosphere but also gases
  • Through the changes in polar air masses it also affects atmospheric circulation

Image sources:

Young Ice (YI)

  • Newly formed ice
  • can be rough or smooth
  • less than 30cm thick

First-year Ice (FYI)

  • Ice that has survived one summer melt season
  • can be level, rough or have ridges
  • 30cm to 2m thick

Multi-year Ice (MYI)

  • Ice that has survived more than one summer melt season
  • typically smoother than FYI
  • Over 2.5m thick and hence protrudes above the waterline
  • has extremely low salinity compared to YI and FYI

Remote Sensing of Sea Ice

Active sensors

  • Radar altimeters (CrysoSat-2)
  • Laser altimeters (IceSat-2)
  • Scatterometers (Metop A/B/C - ASCAT)
  • Synthetic Aperture Radar (Radarsat-2)

Passive sensors

  • Passive microwave radiometers (SMOS)

Hybrid sensors

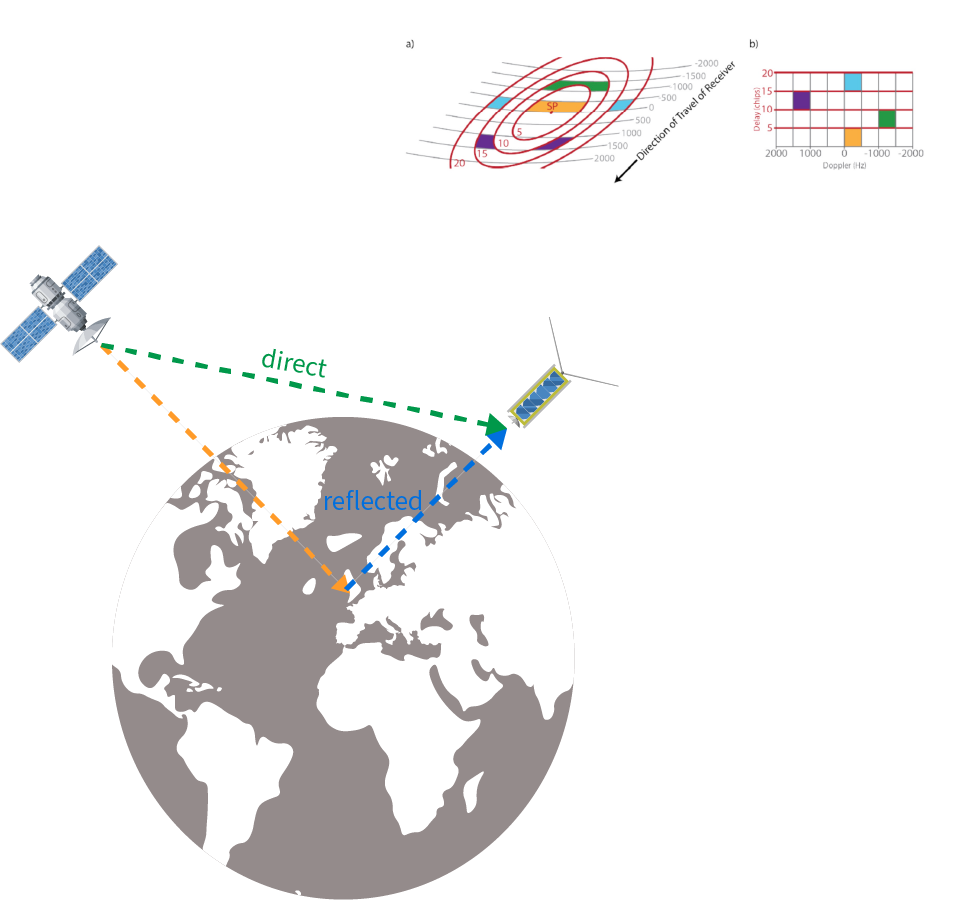
  • Global Navigation Satellite System Reflectometry - GNSS-R

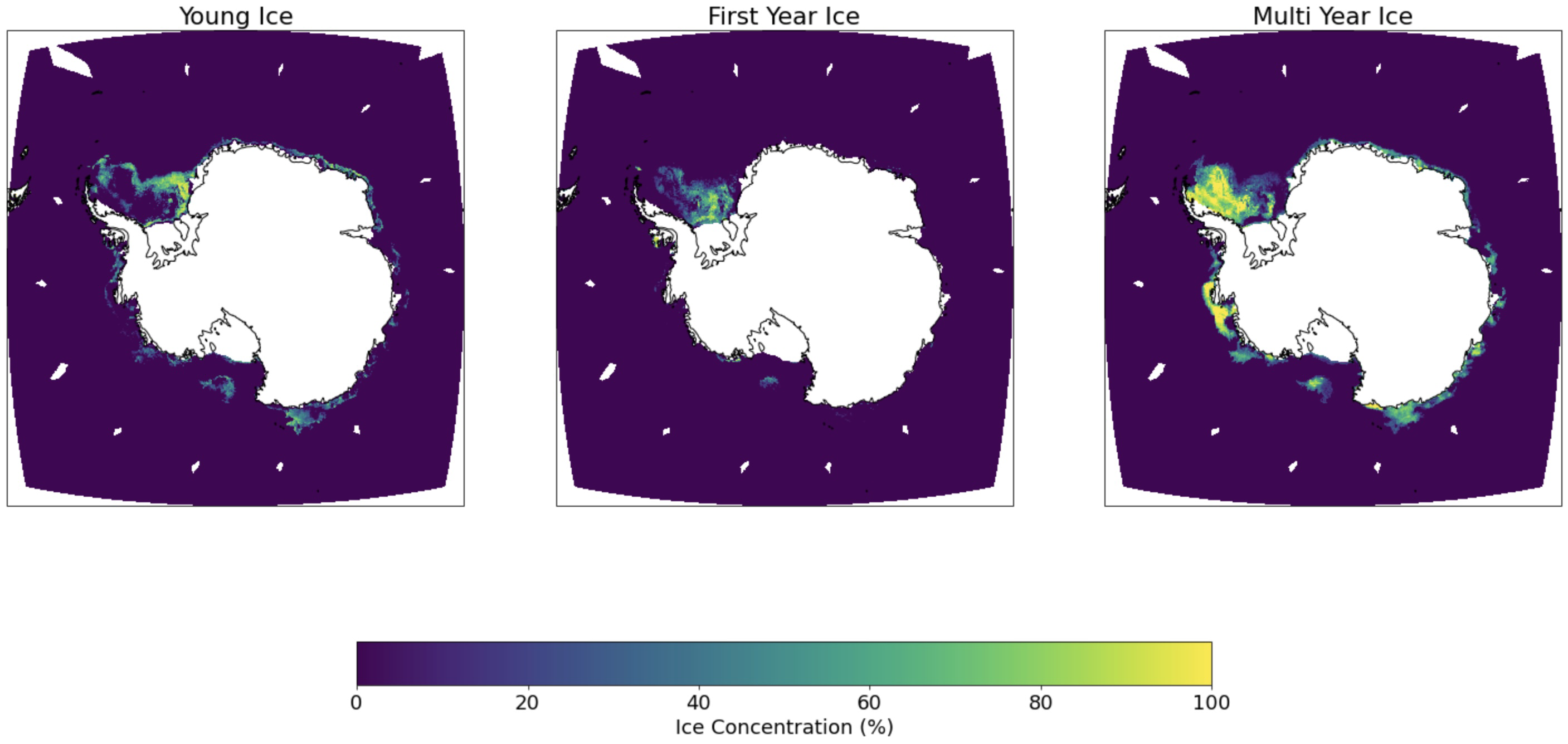
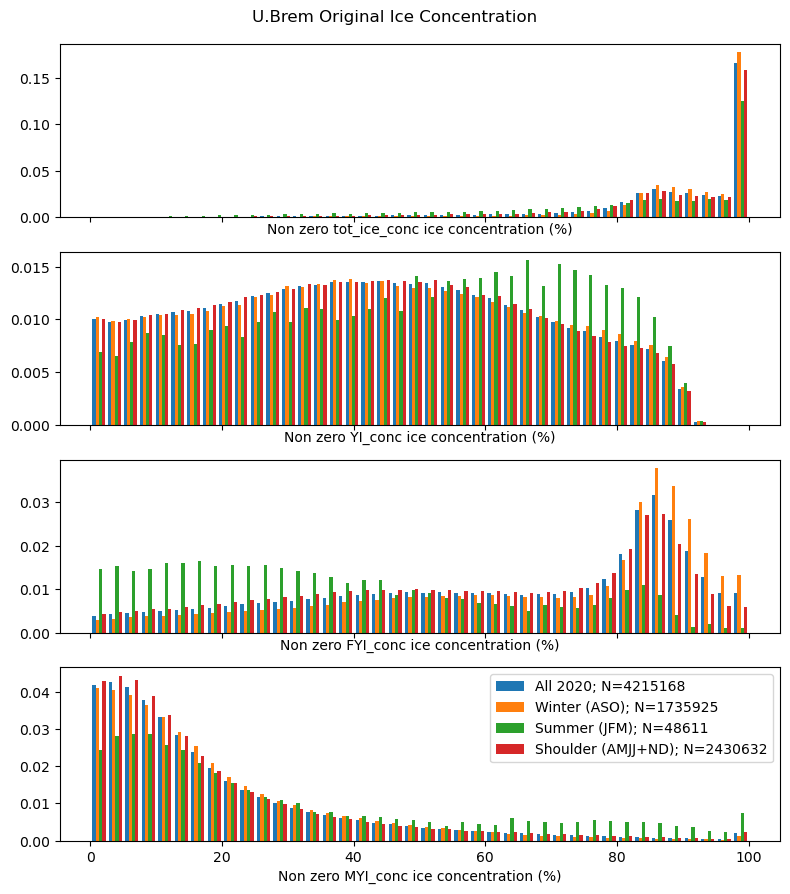
IUP U. Bremen Multiage Ice Concentration

GNSS-R

GNSS-R

IUP Multiyear ice concentration and other sea ice types, Version AQ2 (Antarctic)

  • Provides YI, FYI and MYI concentrations
  • Developed by Institute of Environmental Physics, University of Bremen
  • Uses passive microwave (AMSR2) and scatterometer (ASCAT instruments on Metop A/B/C) data to derive initial estimates
  • Corrects the initial estimates using 2m surface air temperature and sea ice drift data
  • 12.5km x 12.5km grid resolution

Melsheimer, Christian; Spreen, Gunnar; Ye, Yufang; Shokr, Mohammed (2019): Multiyear Ice Concentration, Antarctic, 12.5 km grid, cold seasons 2013-2018 (from satellite). PANGAEA, https://doi.org/10.1594/PANGAEA.909054

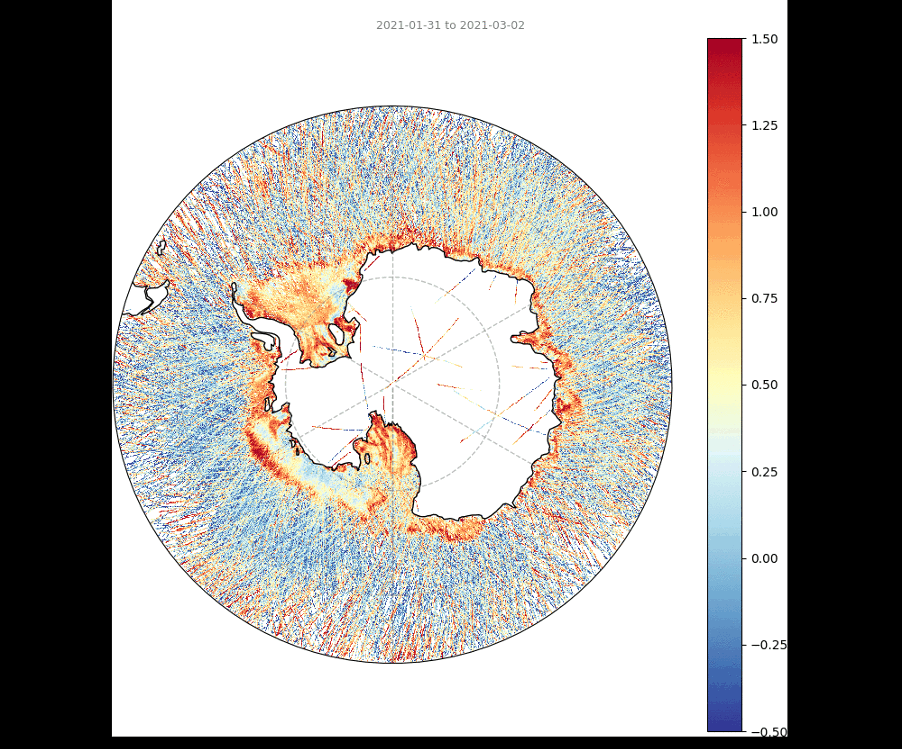
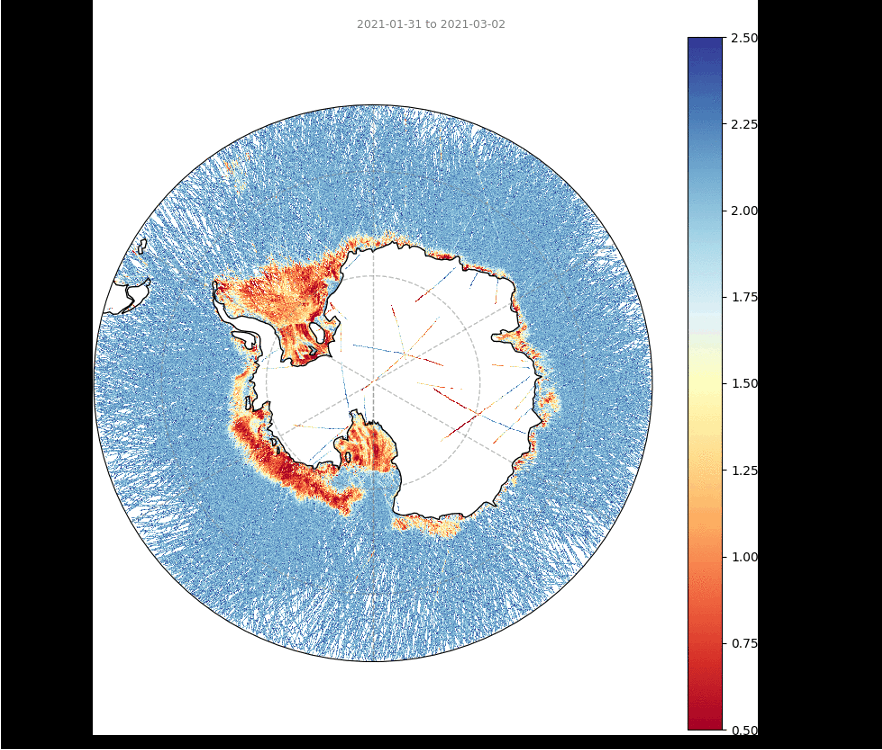
Sea Ice Signal in GNSS-R features?

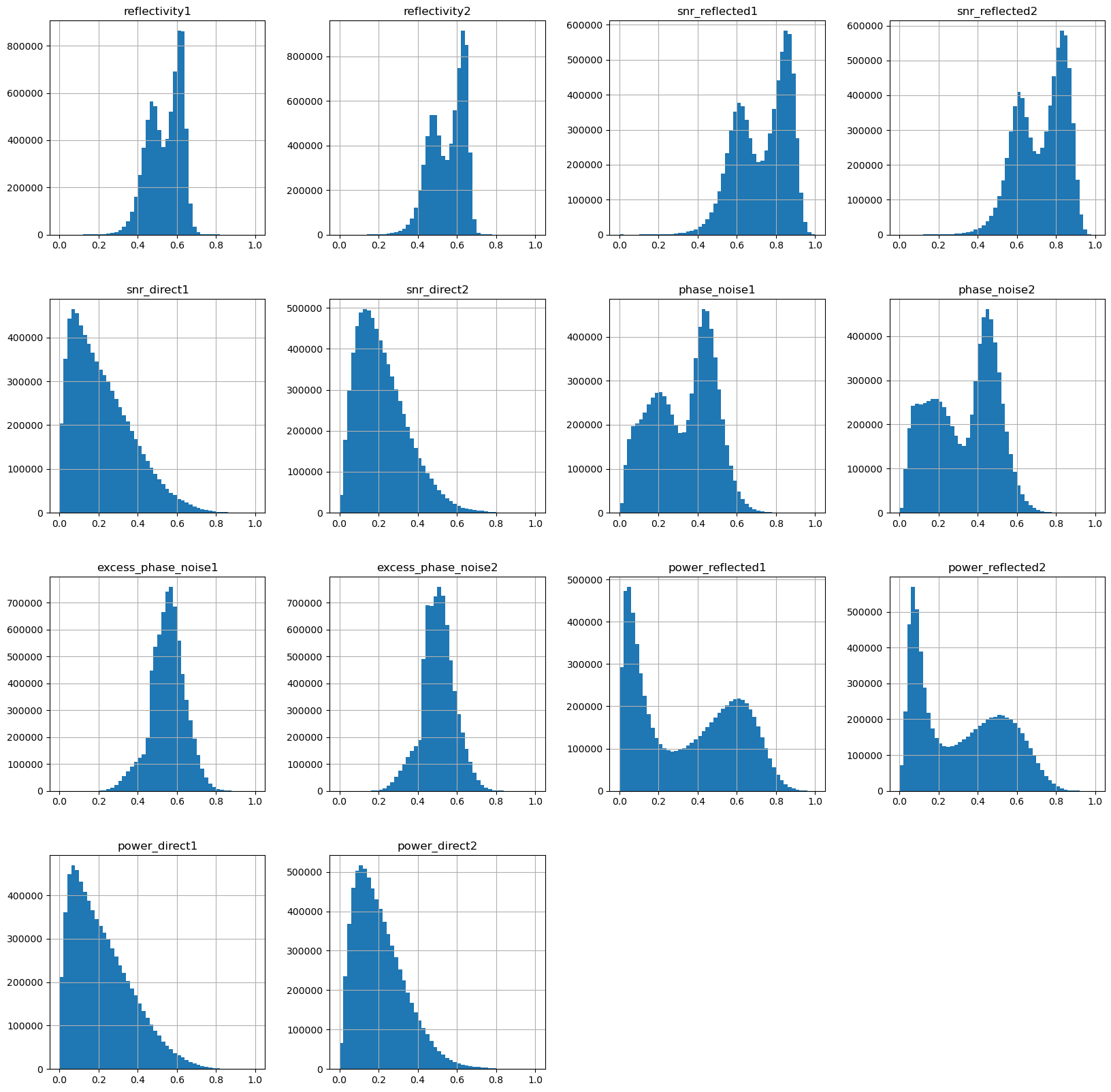
Some details

  • PCA data:
    • water - total ice concentration = 0%
    • ice - total ice concentration > 99%
  • PCA features:
    • reflectivity1
    • snr_reflected1
    • power_reflected1
    • phase_noise1
    • excess_phase_noise1
  • total explained variance: 99.25%

Some details

  • PCA data:
    • YI - YI ice concentration > 90%
    • FYI - FYI ice concentration > 99.9%
    • MYI - MYI ice concentration > 99%
  • PCA features:
    • reflectivity1
    • snr_reflected1
    • power_reflected1
    • phase_noise1
    • excess_phase_noise1
  • total explained variance: 99.58%

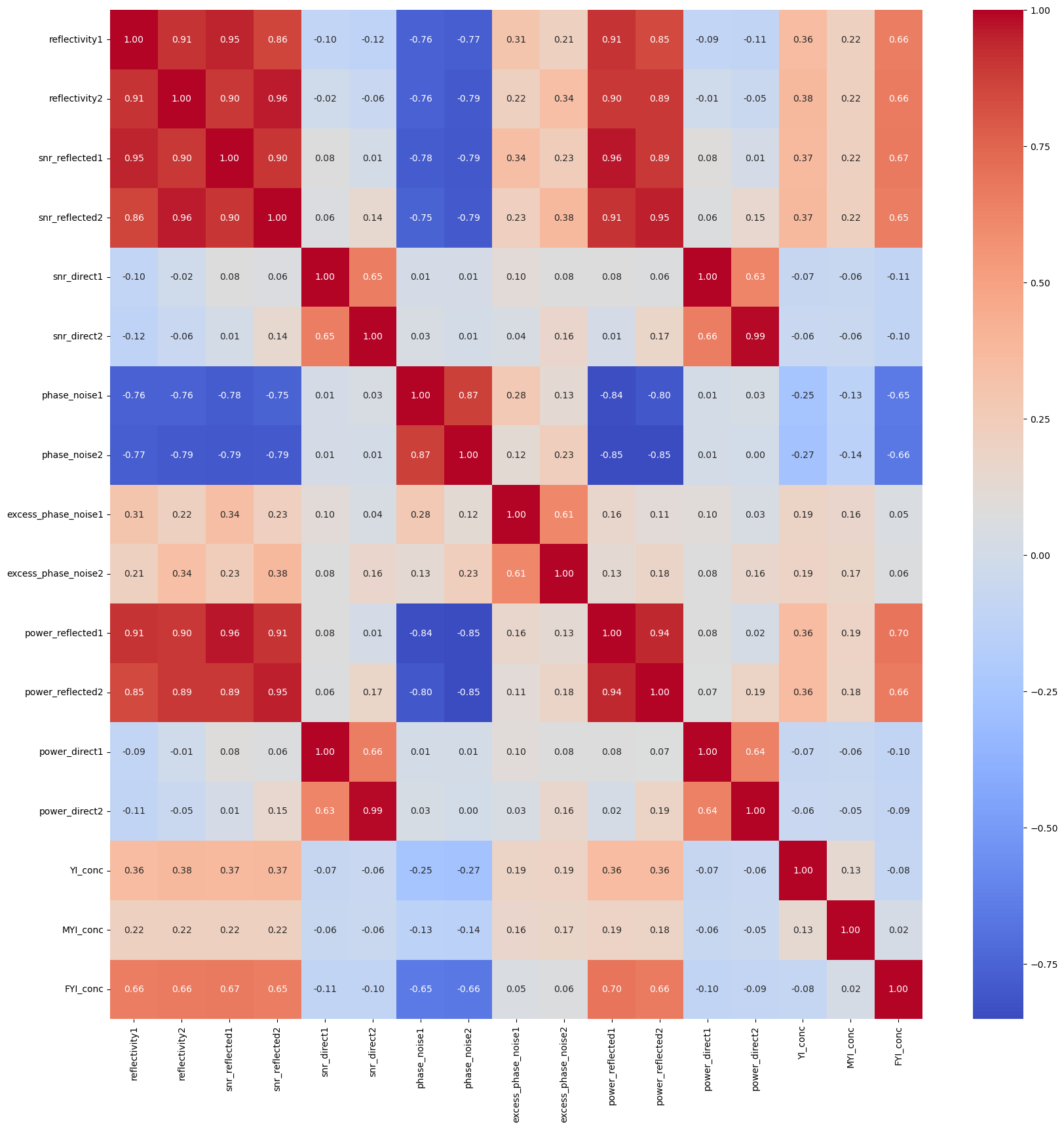
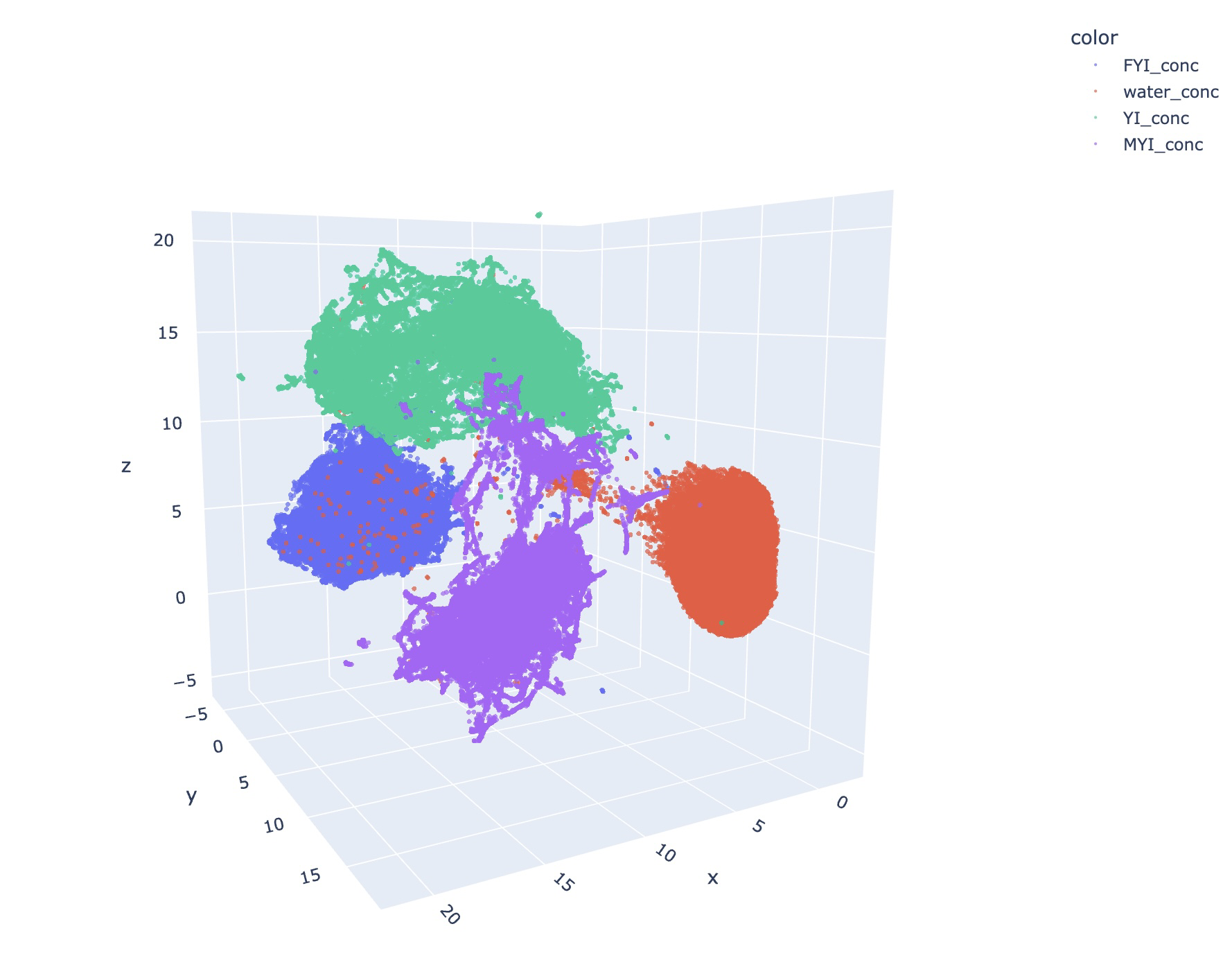
Correlation amongst GNSS-R features and ice types

Geographic distribution

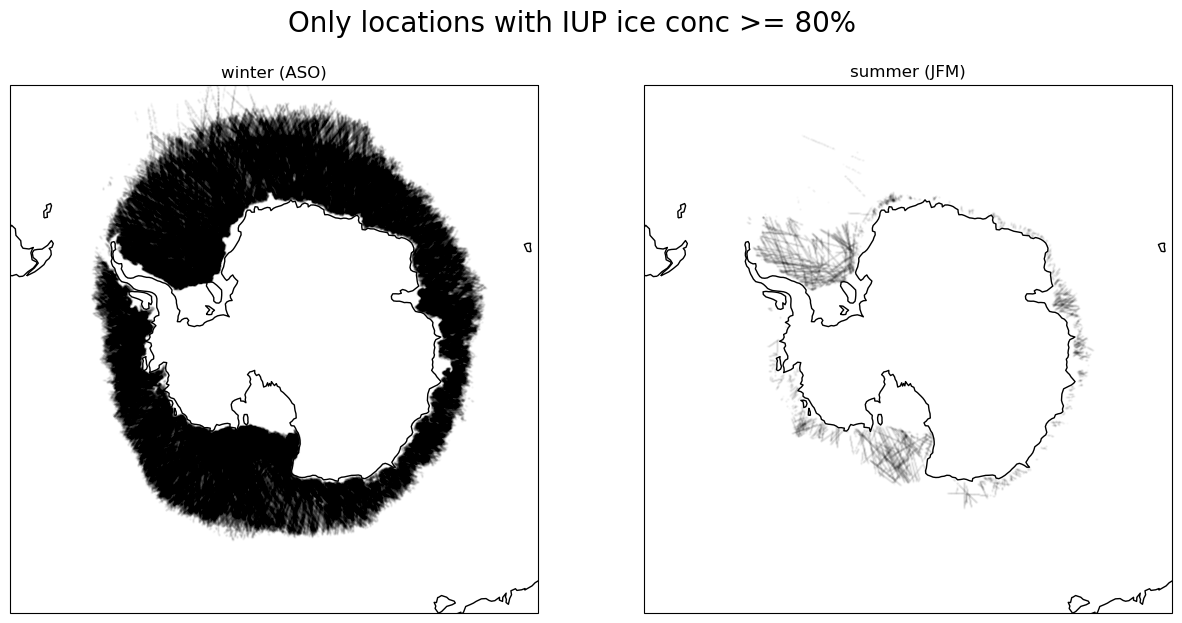
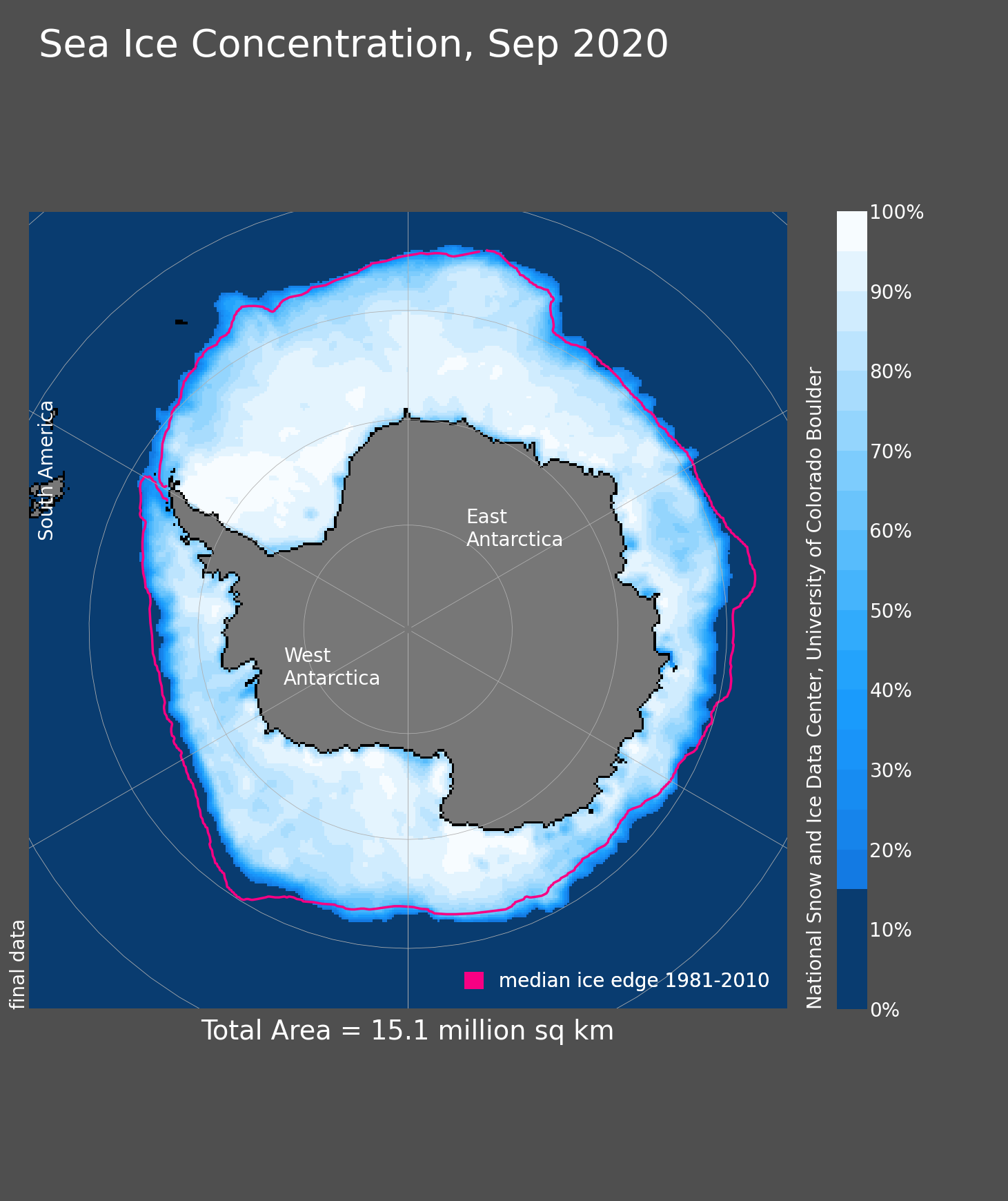
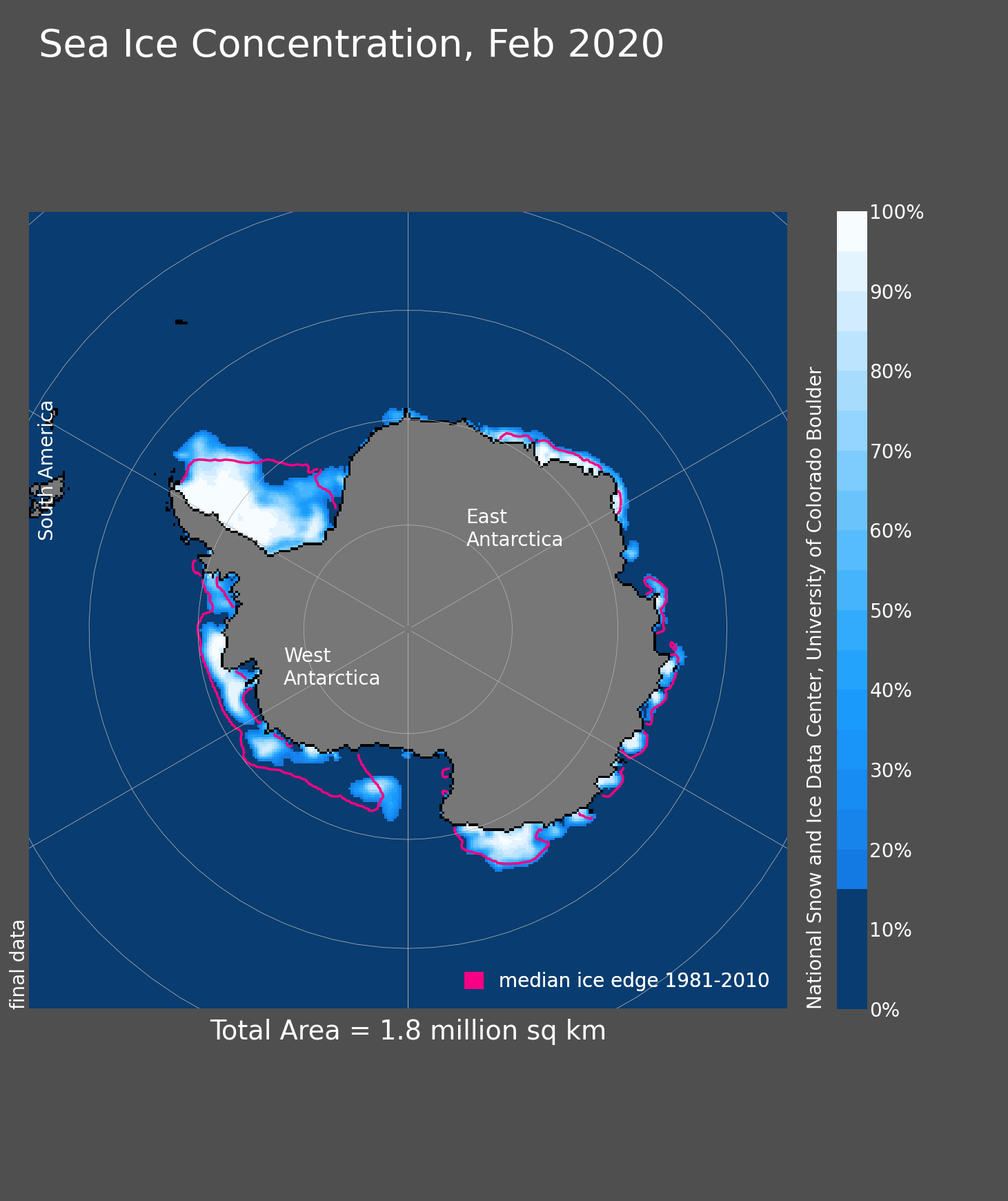
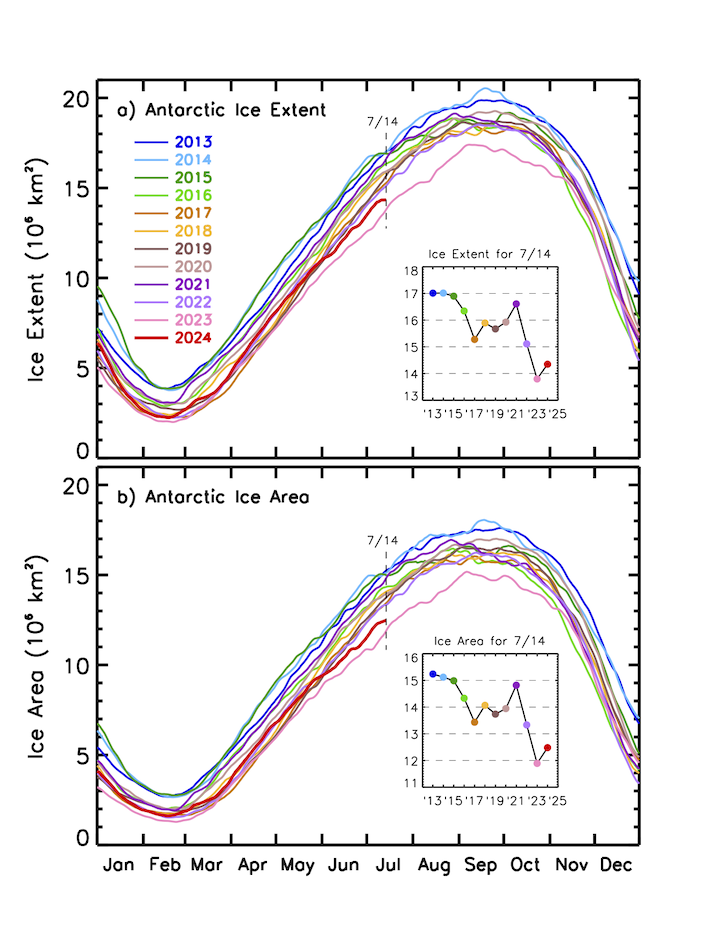
National Snow and Ice Data Center, Boulder, Colorado USA. https://nsidc.org/data/seaice_index, last access: 2024-07-16

J. C. Comiso, A. C. Bliss, R. Gersten, C. L. Parkinson, and T. Markus (2024), Current State of Sea Ice Cover, https://earth.gsfc.nasa.gov/cryo/data/current-state-sea-ice-cover, last access: 2024-07-16.

Ice concentrations as probabilities

  • the spatial footprint of GNSS-R grid is around 2.5% of the size of the IUP grid
  • interprit ice concentration as the probabiliy of seeing that kind of ice inside that grid
  • assume that the ice concentrations can be erroneous
  • assume higher ice concentrations are more likely to be correct
  • semi-supervised approach: learn a mapping from GNSS-R to ice labels where IUP concentrations are close to 100%
  • update the IUP concentrations using the learned mapping

Bayesian update

$$ \begin{align*} P(true\, label\, |\, model\, pred) &= \frac{P(model\, pred\, |\, true\, label) \times P(true\, label)}{P(model\, pred)} \\ &= \frac{P(model\, pred\, |\, true\, label) \times P(true\, label)}{\sum_{true\, labels}{P(model\, pred\, ,\, true\, label)}} \\ &= \frac{P(model\, pred\, |\, true\, label) \times P(true\, label)}{\sum_{true\, labels}{P(model\, pred\, |\, true\, label) \times P(true\, label)}} \end{align*} $$

Two ways to get $P(model\ pred\ |\ true\ label)$:

  • Using a tabular ML model - model calibration required
    • calibrate using test dataset and Bayes rule again
$$ P(pred\ |\ true) = \frac{P(true\ |\ pred)P(pred)}{\sum_{pred\ labels}{P(true\ |\ pred)P(pred)}} $$
  • Using Robust Mixture Discriminent Analysis (RMDA)

Bouveyron, C., & Girard, S. (2009). Robust supervised classification with mixture models: Learning from data with uncertain labels. Pattern Recognition, 42(11), 2649–2658. https://doi.org/10.1016/j.patcog.2009.03.027

Which ML model?

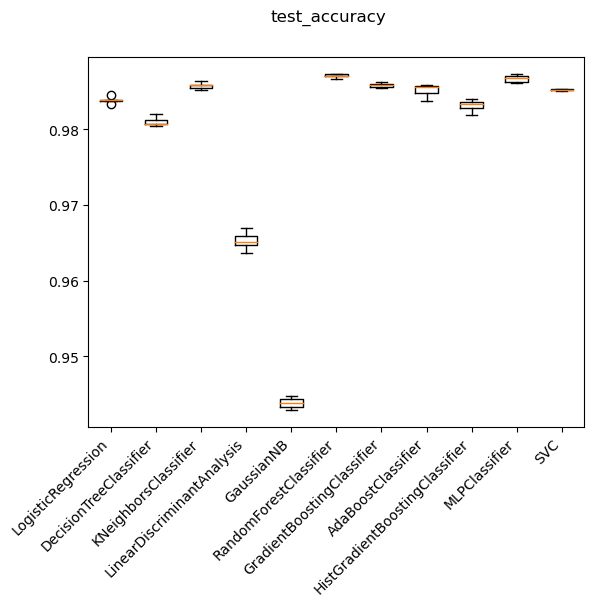
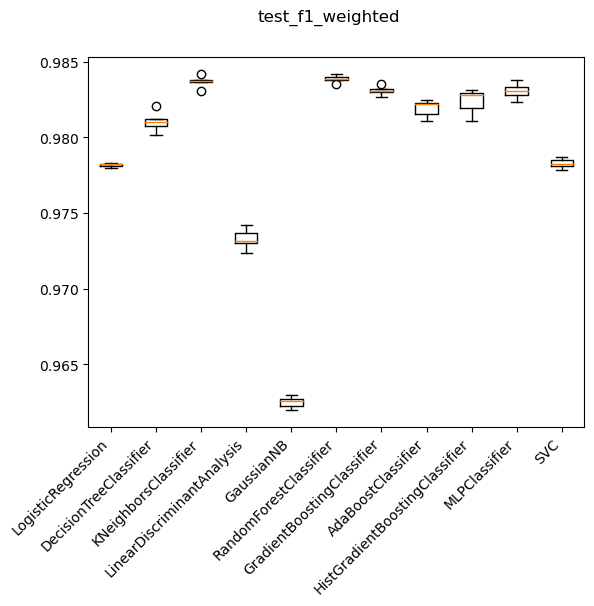
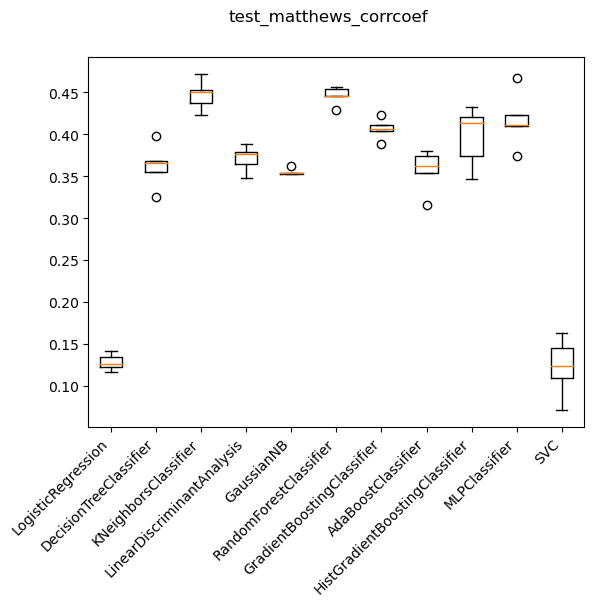
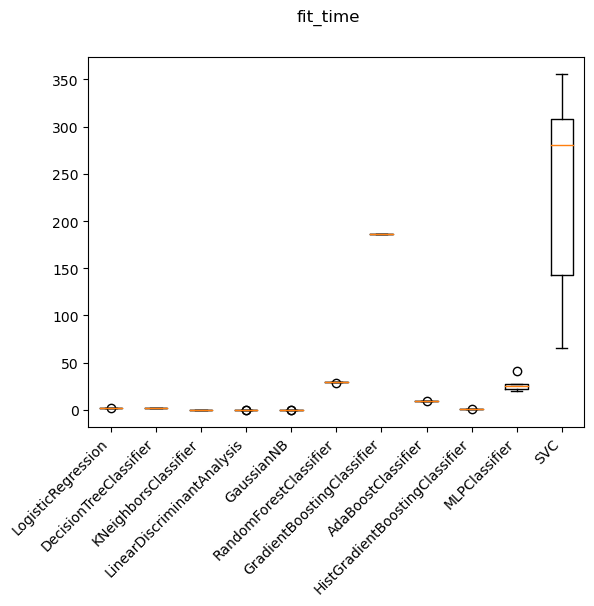
Decision tree ensemble methods

  • Random Forest: Fits an ensemble of N trees on random subsets (known as bagging) of data and predicts with a majority vote.
  • Adaptive Gradient Boosting: Trains N trees sequentially, each tree correcting the errors of the previous tree by weighting the data points that were misclassified. This is known as boosting.
  • Gradient Boosting: Also a boosting method in that it trains N trees sequentially, however, instead of weighting the data points, it fits each tree to the residuals of the previous tree.

LightGBM

Key improvements over vanilla gradient boosting:

  • Histogram-based splitting: LightGBM bins the data points into discrete bins and then splits the bins instead of the data points. This reduces the complexity of the model and speeds up training.
  • Leaf-wise growth: Instead of growing the tree level-wise, LightGBM grows the tree leaf-wise. This reduces the number of nodes in the tree and hence the complexity of the model.
  • Gradient-based One-Side Sampling: LightGBM samples the data points based on the gradient of the loss function. This speeds up training by focusing on the data points that are more informative.
  • Exclusive Feature Bundling: LightGBM bundles exclusive features together to reduce the number of features that need to be considered during training.

Gaussian Mixture Discriminant Analysis

\[ \begin{align*} G &\sim Discrete(K) \\ C &\sim Discrete(L) \\ X &\in \mathbb{R}^p \\ p(x|C=i) &= \sum_{j=1}^{K} P(C=i,G=j)p(x|G=j) \\ p(x) &= \sum_{i=1}^L\sum_{j=1}^{K} P(C=i,G=j)p(x|G=j) \\ &= \sum_{i=1}^L\sum_{j=1}^{K} \pi_{ij}\phi(x;\mu_ij,\Sigma_ij) \end{align*} \] Here $\pi_{ij}$ is the mixing coefficient such that $\sum_{j=1}^K \pi_{ij} = 1$, and $\phi(x;\mu_ij,\Sigma_ij)$ is the multivariate Gaussian distribution with mean $\mu_ij$ and covariance $\Sigma_ij$.

Robust Mixture Discriminant Analysis

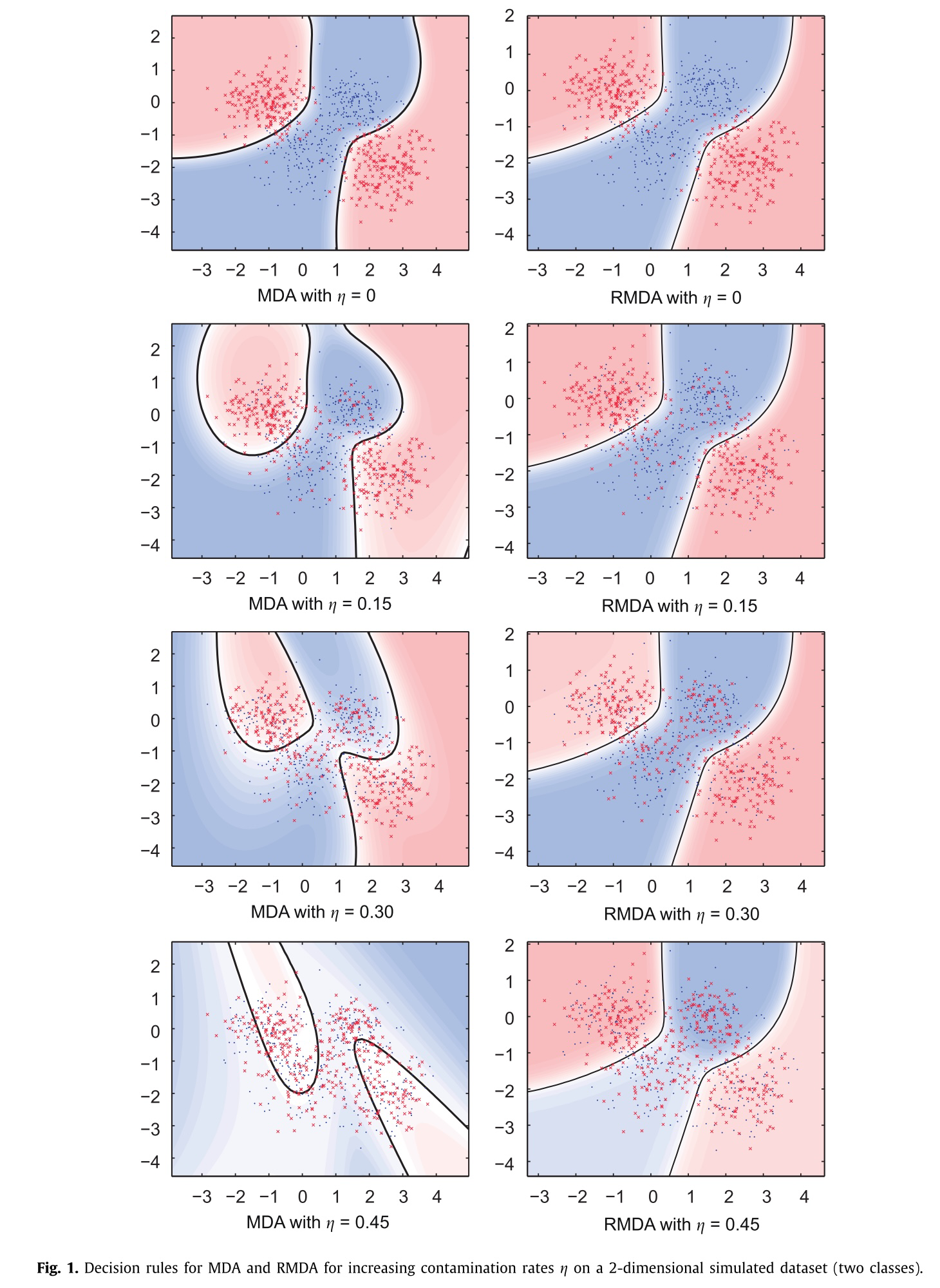
\[ \begin{align*} p(x) &= \sum_{i=1}^L\sum_{j=1}^{K} P(C=i,G=j)p(x|G=j) \\ &= \sum_{i=1}^L\sum_{j=1}^{K} P(C=i|G=j)P(G=j)p(x|G=j) \\ &= \sum_{i=1}^L\sum_{j=1}^{K} r_{ij}\pi_j\phi(x;\mu_j,\Sigma_j) \end{align*} \] Since $\pi_j$ does not depend on $C$, we can fit a gaussian mixture model (unsupervised) to get $\pi_j$. To get the, $L\times K$, matrix $R=(r_{ij})$ parameters, we maximise the log likelihood: \[ l(R) = \sum_{i=1}^{L}\sum_{x\in \mathcal{C}_i} log(R_i\Psi(x)) \] where $\Psi(x) = (P(S=1|X=x),P(S=1|X=x),...,P(S=K|X=x))^t$ and $\mathcal{C}_i=\{x_l\}$ such that $x_l$ belongs to class $C=i$, w.r.t. $r_{ij}\in [0,1], \forall i\in {1,...,L}\text{ and }j\in{1,...,K}$, subject to $\sum_{i=1}^{L} r_{ij}=1, \forall j=1,...,K$.

Class rebalancing

  • Training score: 83.7%
  • Validation score: 81.3%
YIFYIMYIwater
YI0.592378750.279445730.03695150.09122402
FYI0.028846150.943461540.018846150.00884615
MYI0.088863890.649043870.224971880.03712036
water0.028490030.017450140.007478630.9465812
  • The entire dataset contains 7.39M rows.
  • After filtering rows where we have high confidence in labels (YI>90%, FYI>99.9%, MYI>99.%,Water=100%), we are left with:
    • YI: 9801 rows
    • FYI: 28266 rows
    • MYI: 9805 rows
    • Water: 3.18M rows

Solution: SMOTE based class rebalancing

SMOTE

  • Synthetic Minority Over-sampling Technique
    1. Identify the minority class
    2. Find its nearest neighbours
    3. Generate synthetic samples by interpolating between the minority class and its neighbours
  • After SMOTE each class contains 3.18M rows
  • So we randomly undersampled and treated the number of samples in each class as a hyperparameter
  • More sophisticated undersampling techniques (Tomek, Edited Nearest Neighbours) did not prune the dataset enough

Performance after class rebalancing

Number of resampled rows in each class~1.6M
Training accuracy99.34%
Validation accuracy99.12%
Test accuracy96.34%

Test Confusion matrix

YIFYIMYIwater
YI0.672413790.159229210.041582150.12677485
FYI0.047904190.846777030.085593520.01972526
MYI0.0468750.258789060.642578120.05175781
water0.017412540.009942830.006264610.96638002

Updated ice probability density

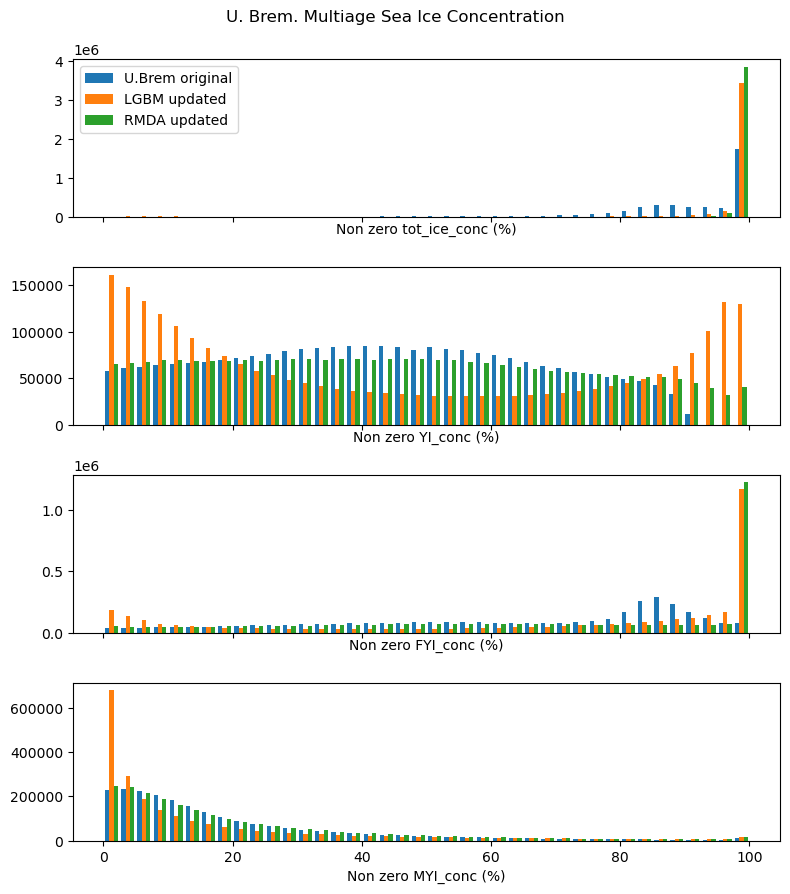
UMAP (Uniform Manifold Approximation and Projection)

  • UMAP is a non-linear dimensionality reduction technique that is particularly well-suited for visualizing complex data in a low-dimensional space
  • UMAP assumes that high-dimensional data lies on a low-dimensional manifold embedded in the higher-dimensional space
  • UMAP first constructs a weighted k-nearest neighbor graph from the high-dimensional data
  • UMAP then defines a low-dimensional representation and uses stochastic gradient descent to optimize the layout of the low-dimensional points, preserving the structure of the high-dimensional graph as closely as possible
  • It thus preserves both local and global structure of the data
  • Supervised mode:
    • During knn graph construction, UMAP uses the labels to weight the edges in the graph so that points with the same label are closer in the low-dimensional space
    • Also adds a loss term to the optimization function that penalizes points with the same label being far apart in the low-dimensional space

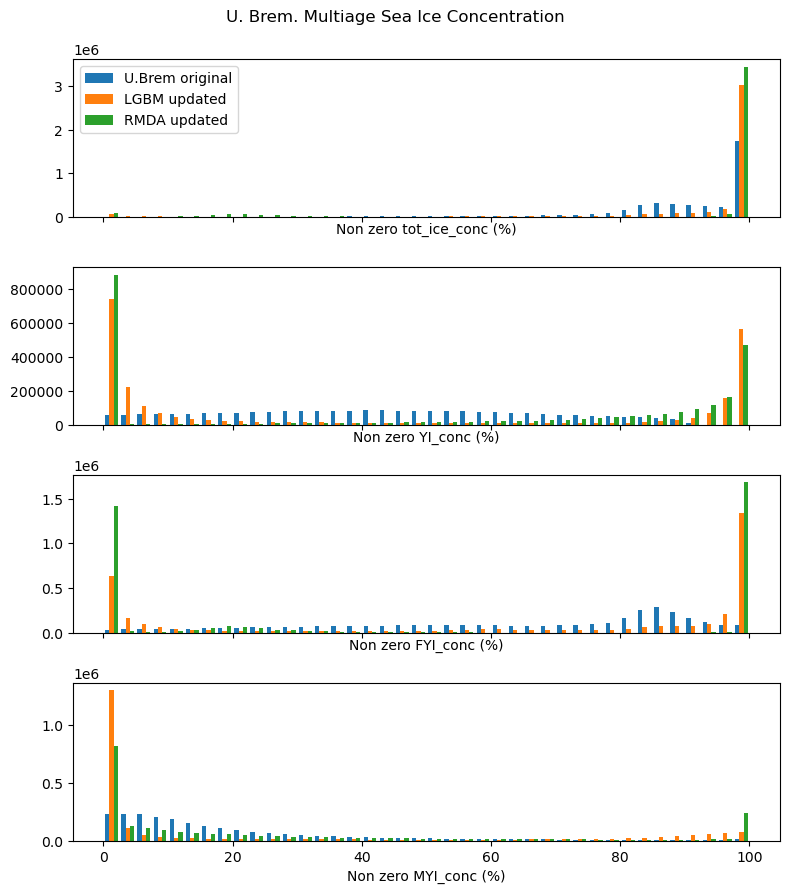
Performance after UMAP feature transformation

Number of resampled rows in each class~300K
Training accuracy99.99%
Validation accuracy99.84%
Test accuracy93.34%

Test Confusion matrix

YIFYIMYIwater
YI0.958669350.021169350.01411290.00604839
FYI0.012432010.956487960.021756020.00932401
MYI0.012084590.028197380.951661630.00805639
water0.045242510.009518450.021065780.92417327

Updated ice probability density

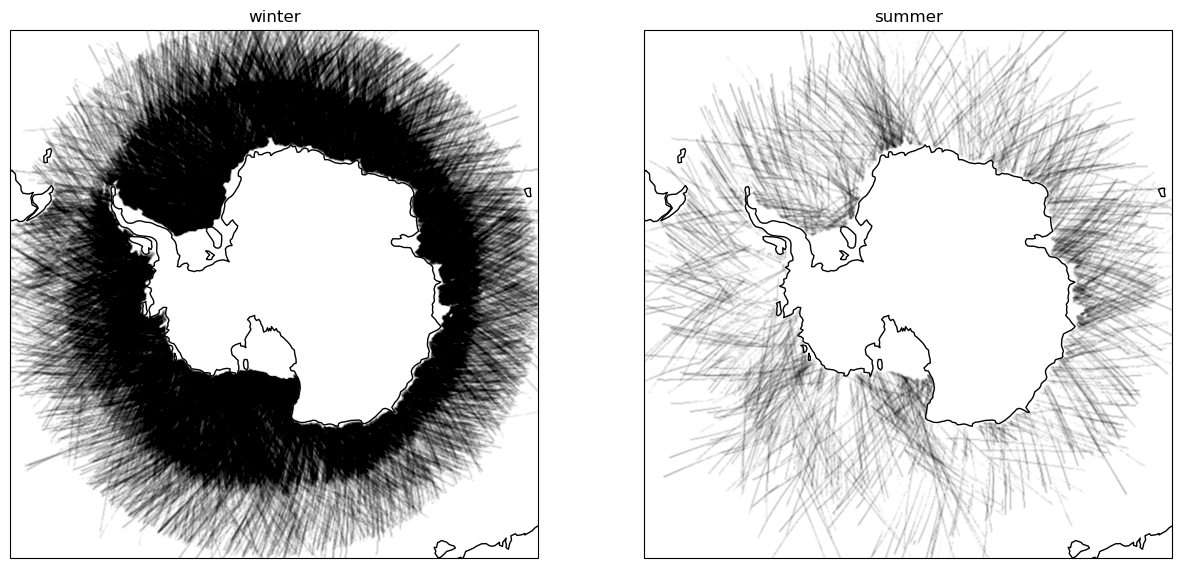
Updated geographic distribution - winter

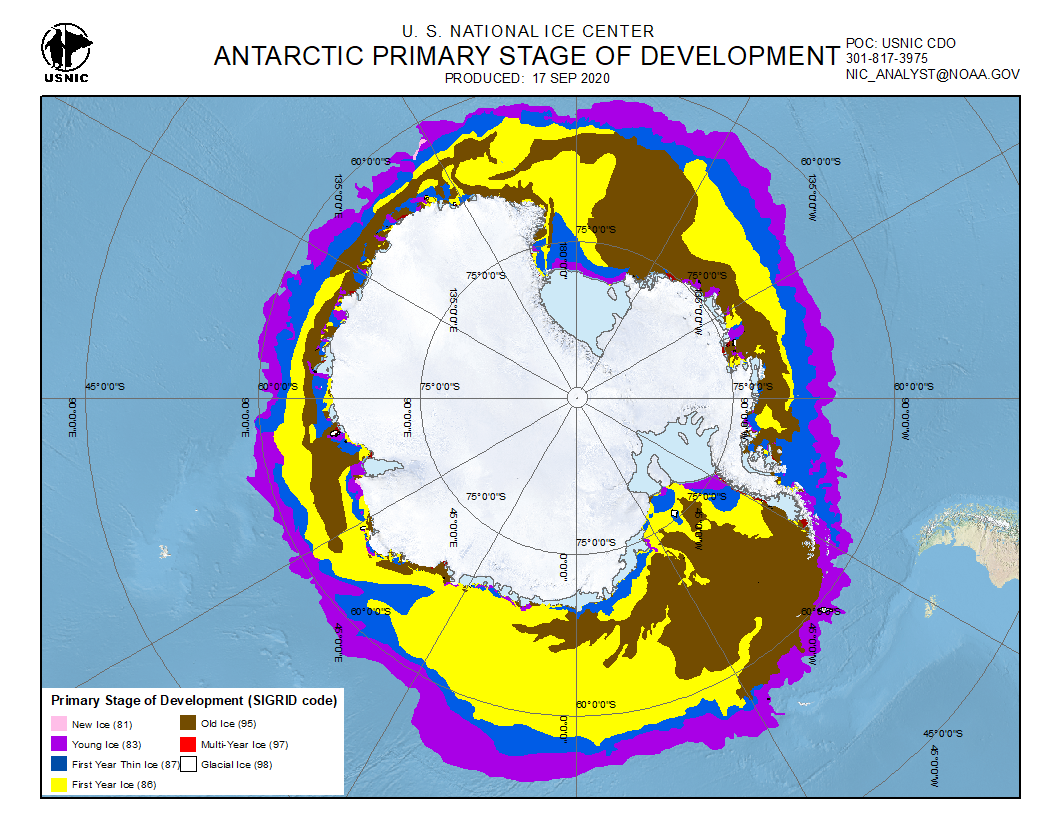
Updated geographic distribution - summer

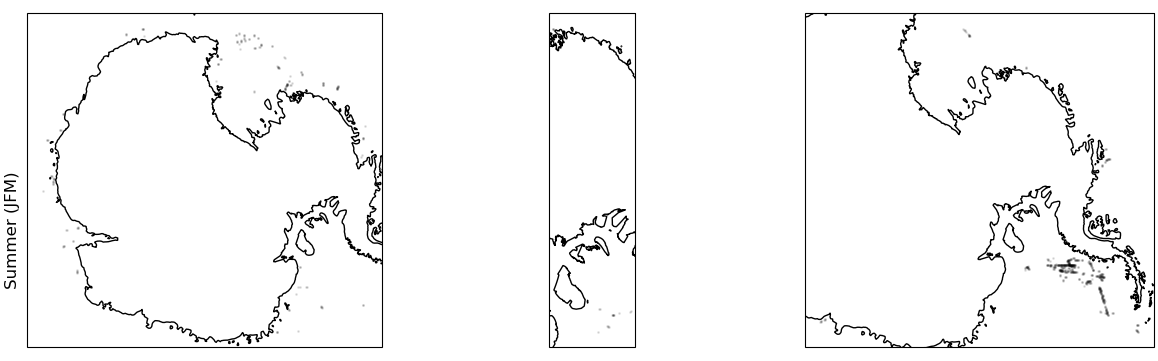
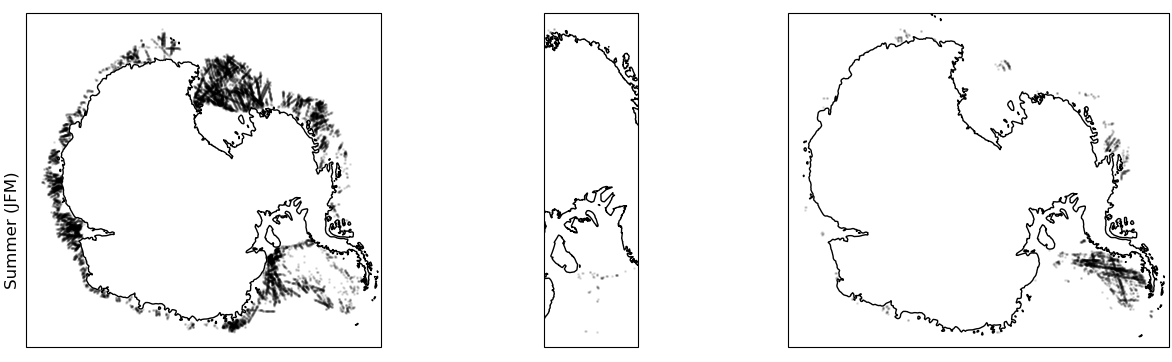
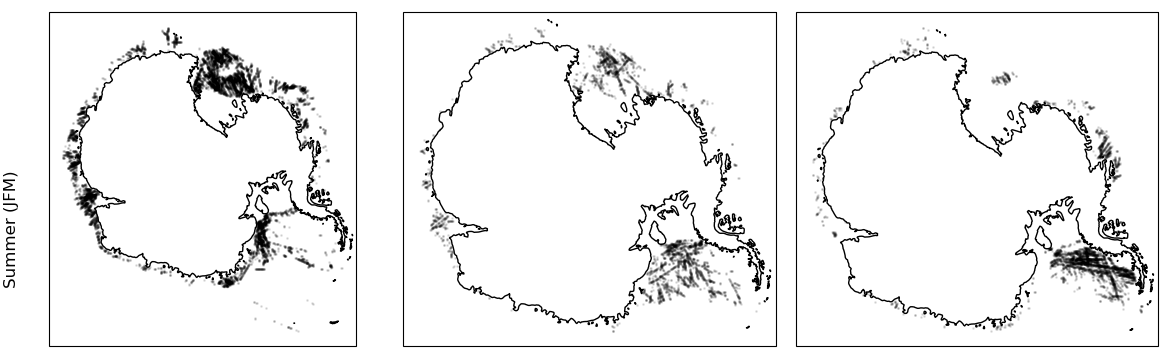
  • GNSS-R is an exciting new data source for monitoring sea ice at very high resolution
  • we fitted models to predict ice types and used these models to update existing ice concentration datasets
  • we pick up many more locations previously missed thus improving existing ice concentration datasets
  • this was only one year of data, the accuracy will improve with more data

More validation required! We are open to ideas

Thank you